Приходит давеча ко мне дочь, и делится очередным любопытным фактом, который где-то вычитала.
- "Папа, а ты знаешь, что если взять весь грибной мицелий на планете Земля, и сделать из него ниточку, то эта ниточка будет длиной в половину нашей галактики? А, и кстати... пап, что такое мицелий?" )))
Ну про мицелий я ей объяснил как умел, а вот про ниточку с галактикой стало любопытно. А что если бы наша Земля была гигантским клубком ниток - какой длины была бы эта нитка? А вдруг окажется что она и до половины галактики не дотягивает, и моему ребенку нагло напи... наврали? Ща батя разберется.

Итак, чтобы размотать нашу планетку, нам надо взять ее объем, и растянуть его в сечении среднестатистической нитки. Гуглим объем Земли

1 083 210 000 000 км3

Теперь надо узнать площадь сечения среднестатистической нити. Оказывается, толщина ниток указывается в каких-то дурацких дробях, где указывается сколько метров содержится в 1 грамме ниток, но нам то нужен диаметр в миллиметрах! Короче, еще погуглив выяснилось что диаметр самой ходовой нитки 40/2 примерно 0.3мм. По формуле площади круга получаем площадь сечения нитки 0.0707мм2. А следовательно, 1 метр нитки будет иметь объем 0.0707 х 1000 = 70.7мм3

Теперь можно прикинуть какой длины будет, например, кубометр ниток. В кубометре один миллиард кубомиллиметров, а значит 1 000 000 000 / 70.7 ≈ 14 144 271 метр, или 14 с лишним тысяч километров! Т.е. тремя кубометрами ниток можно обмотать земной шар по экватору (и еще на варежки останется). А в кубическом километре нитки уже на 14.144 триллиона километров длины, или полтора световых года!

Дело за малым - берем объем Земли который нагуглился вначале, и умножаем на полтора. Получаем длину в световых годах нитки клубка размером с Землю - 1,625 ТРИЛЛИОНА СВЕТОВЫХ ЛЕТ. Диаметр наблюдаемой Вселенной, по последним оценкам - около 93 миллиардов световых лет, т.е. нашей ниточки хватило бы на то чтобы ПЯТЬ С ПОЛОВИНОЙ РАЗ обмотать сферу наблюдаемой Вселенной.

Ну значит норм, про мицелий скорее всего не наврали, батя спокоен.

В общем, я хз зачем вам (да и мне) эта информация, но уже всё. Живите теперь с этим.

Заказал на вайлдберрис фольгу. Пищевую. Алюминиевую. 50 метров, 44 см шириной и толщиной 20 мкм. ( не знаю нахрена мне такая толстая фольга, не спрашивайте). Пришла запечатанная в полиэтилен, без каких-либо опознавательных знаков.

И хрен бы на эту фольгу, но попался мне отзыв.

Стало интересно, а соответствует ли фольга заявленным характеристикам, есть ли там 20 мкм, и 50 метров длины. Вспомнил, что уже лет пять в чемодане с инструментами ждет своего часа микрометр.

Видим что заявленная толщина и измерения практически совпадают. Не плохо.
Разматывать весь рулон, чтоб проверить длину не разрешила жена не стал, а решил отмерить погонный метр

взвесить его. 23,1 гр.

Взвесить весь рулон. 1236 гр.

23,1 гр*50 метров=1155 гр должы весить 50 метров. По факту 1236 гр. Не забываем что внутри картонная втулка.

Касательно длины вопросов больше нет, а как бы точнее узнать толщину? Знаем вес, знаем два из трех измерения, узнаем в интернете удельный вес алюминия 2,698 гр/см3.

23,1гр/100см/44см/2,698гр/см3=19,5мкм. Приемлемо, учитывая погрешность весов и мой кривой рез.
Вывод. Фольга соответствует заявленным характеристикам, а Александр, который оставил отзыв, пусть пощупает что-нибудь другое.

Есть у меня дома песочные часы из (без)временно покинувшей нас IKEA.

Вот такие.

Тикают ровно две минуты (плюс-минус секунда).

Стояли тихо-мирно в спальне у дочки, и в один прекрасный день она озадачила меня вопросом:

- Пап, а сколько там внутри этих песчинок?

Эммм... нууу... а правда, сколько? Десять тысяч? Двадцать?

Я по быстрому прикинул - раз они пересыпаются за 120 секунд, а в секунду их пересыпается... нуууу... пусть штук 200... значит где-то 25 тысяч наверно? Ну в крайнем случае тысяч 30. Озвучил это число дочери, она вроде успокоилась.

А Я НЕТ.

Поэтому решил немного упороться, и хотя бы примерно посчитать количество этих "песчинок"

Т.к. "песчинки" в этих часах ненастоящие, а что-то типа крохотных шариков, то для того чтобы  приблизительно представить сколько их там штук, можно посчитать объем, который они занимают, затем разделить на средний объем одного шарика, и умножить на коэффициент плотности упаковки шаров (т.к. шарики занимают не весь объем, между ними остается свободное пространство). С этого коэффициента и начнем.

В идеальном случае этот коэффициент рассчитал еще Карл Фридрих Гаусс, и у него получилось что-то около 74%. Но в реальности, естессно, так не бывает. Погуглив, и едва не погрязнув в жутком матане, я нашел статью об опытах какого-то Г.Скотта, который от нехер делать заполнял разные бутыли шариками от подшипников, а потом вывел красивую зависимость плотности шариков в объеме от их количества. Причем у него получилось вывести даже две зависимости - для случая если в ёмкость просто засыпать шарики, и если если емкость еще при этом потряхивать... Эх, золотой был человек.

Мне нужна как раз вторая, "потряхиваемая"

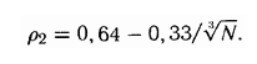
Т.к. у нас число шариков N - многие тыщи, то можно вообще забить и взять этот коэффициент за 0.64

Теперь надо прикинуть объем, который занимает эта масса шариков. Это самая дурацкая задача, т.к. сосуд этих часов несмотря на внешнюю простоту имеет очень хитрожопую форму с переходами к скошенным углам, поэтому после нескольких попыток посчитать объем этой конструкции я забил, и решил считать как обычную шестигранную чашу, сильно на результат это не повлияет. Размеры снимал штангенциркулем.

Площадь дна получилась 28.53 см2, высота объема шариков (после потряхивания естессно) - 32мм. Итого объем шариковой массы - 91.296 см3

Дело за малым - найти средний объем одного шарика. Т.е. надо измерить средний диаметр этих "песчинок". Я не придумал ничего умнее, чем сфоткать их на фоне линейки, и по пикселям прикинуть средний размер 

Измерив пару десятков рандомных шариков на изображении получилось, что разрешении 50 пикселей на мм, средний диаметр шарика составил 49.5 39.5 пикселей, что дает нам диаметр сферы 0.79мм, а значит средний объем одной такой "песчинки" - 0.2581мм3, или 0.0002581см3

Итак, мы подошли к самому главному.

Берем объем всей массы, делим его на средний объем одного шарика, и умножаем на коэффициент заполнения:

91.296 / 0.0002581 * 0.64 = 226382 !

Охренеть. Т.е. изначально я ошибся почти на порядок.

В общем, я не знаю зачем вам (да и мне) эта инфа, но теперь вы знаете - в песочных часах из Икеи примерно 230 тысяч шариков, а за секунду работы этих часов через их крошечное отверстие пролетает примерно 1900 песчинок.

Живите теперь с этим.